How To Find The Area Of The Triangle Formula
Ronan Farrow
Feb 24, 2025 · 3 min read
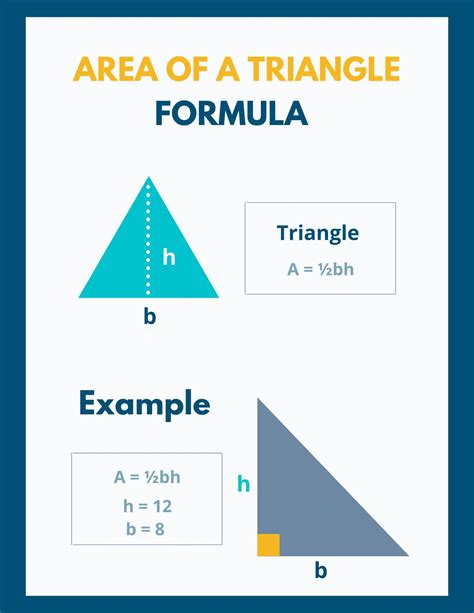
Table of Contents
How to Find the Area of a Triangle: A Comprehensive Guide
Finding the area of a triangle might seem like a simple task, but understanding the different formulas and when to apply them is crucial. This comprehensive guide will walk you through various methods, ensuring you can confidently tackle any triangle area problem.
Understanding the Basics: What is Area?
Before diving into formulas, let's establish a foundational understanding. The area of a triangle represents the amount of two-dimensional space enclosed within its three sides. It's measured in square units (e.g., square centimeters, square meters, square inches).
The Most Common Formula: Base and Height
The most widely used formula for calculating the area of a triangle relies on its base and height:
Area = (1/2) * base * height
- Base: This is any one of the triangle's three sides. It's usually the side that sits horizontally at the bottom.
- Height: This is the perpendicular distance from the base to the opposite vertex (the highest point of the triangle). Crucially, the height must form a right angle (90 degrees) with the base.
Example:
Imagine a triangle with a base of 6 cm and a height of 4 cm. Applying the formula:
Area = (1/2) * 6 cm * 4 cm = 12 cm²
When the Height Isn't Directly Given: Heron's Formula
Sometimes, you might not be given the height directly. In such cases, Heron's formula proves invaluable. This formula utilizes the lengths of all three sides (a, b, and c) to calculate the area.
First, you need to find the semi-perimeter (s):
s = (a + b + c) / 2
Then, apply Heron's formula:
Area = √[s(s-a)(s-b)(s-c)]
Example:
Let's say a triangle has sides of length 5, 6, and 7 cm.
-
Calculate the semi-perimeter (s): s = (5 + 6 + 7) / 2 = 9 cm
-
Apply Heron's formula: Area = √[9(9-5)(9-6)(9-7)] = √[9 * 4 * 3 * 2] = √216 ≈ 14.7 cm²
Using Trigonometry: Area with Two Sides and Included Angle
If you know the lengths of two sides (a and b) and the angle (θ) between them, you can use trigonometry:
Area = (1/2) * a * b * sin(θ)
This formula is particularly useful when dealing with triangles where the height isn't easily determined.
Example:
Suppose you have two sides of lengths 8 cm and 10 cm, with an included angle of 30 degrees.
Area = (1/2) * 8 cm * 10 cm * sin(30°) = 20 cm² (Remember that sin(30°) = 0.5)
Choosing the Right Formula: A Summary
The best formula to use depends entirely on the information you're given:
- Base and Height: Use this when you have the base and the perpendicular height. This is usually the easiest and most straightforward method.
- Three Sides: If you only have the lengths of all three sides, Heron's formula is your go-to option.
- Two Sides and Included Angle: When you know two sides and the angle between them, the trigonometric formula provides an efficient solution.
Mastering Triangle Area Calculations
Understanding these formulas and knowing when to apply each one is crucial for success in geometry and related fields. By practicing with various examples, you'll build confidence and proficiency in calculating the area of any triangle. Remember to always double-check your calculations and units for accuracy.
Featured Posts
Also read the following articles
| Article Title | Date |
|---|---|
| How To Put Image Into Illustrator | Feb 24, 2025 |
| How To Train Your Dragon Live Action Studio | Feb 24, 2025 |
| How To Reset Iphone Data | Feb 24, 2025 |
| How To Keep Iphone Battery Health At 100 | Feb 24, 2025 |
| How To Make Cold Brew Coffee Less Acidic | Feb 24, 2025 |
Latest Posts
Thank you for visiting our website which covers about How To Find The Area Of The Triangle Formula . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
