How To Find Acceleration Of Yoyo
Ronan Farrow
Feb 24, 2025 · 3 min read
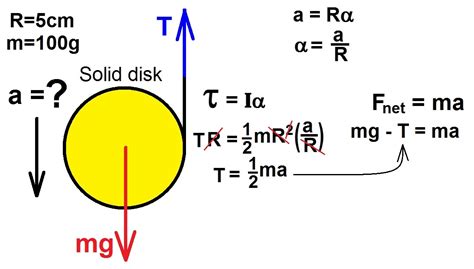
Table of Contents
How to Find the Acceleration of a Yo-Yo: A Complete Guide
The seemingly simple yo-yo hides a fascinating world of physics. Understanding its motion involves grasping concepts like linear acceleration, rotational acceleration, and the interplay between gravity, tension, and inertia. This guide will walk you through how to calculate the acceleration of a yo-yo, breaking down the process step-by-step.
Understanding the Forces at Play
Before diving into the calculations, let's identify the key forces acting on a yo-yo as it unwinds:
-
Gravity (Fg): This force pulls the yo-yo downwards, causing it to accelerate. Its magnitude is simply mg, where m is the mass of the yo-yo and g is the acceleration due to gravity (approximately 9.8 m/s²).
-
Tension (T): The string exerts an upward tension force on the yo-yo. This force opposes gravity and is crucial in determining the yo-yo's acceleration.
-
Inertia: The yo-yo's resistance to changes in its motion. This is particularly important because the yo-yo is not just translating (moving linearly); it's also rotating.
Deriving the Equation for Linear Acceleration
To determine the linear acceleration (a), we'll use Newton's second law of motion (ΣF = ma) and consider both translational and rotational motion. The net force acting on the yo-yo is the difference between gravity and tension:
ΣF = Fg - T = ma
However, the tension also creates a torque (τ) that causes the yo-yo to rotate. The torque is given by:
τ = Iα
Where:
- τ is the torque
- I is the moment of inertia of the yo-yo (this depends on its shape and mass distribution)
- α is the angular acceleration
The relationship between linear and angular acceleration is:
α = a/r
Where r is the radius of the yo-yo.
Substituting these equations, we can derive an expression for the linear acceleration (a):
a = g(m/(m + I/r²))
This equation shows that the yo-yo's linear acceleration is less than g due to the rotational inertia of the yo-yo. A larger moment of inertia (I) results in a smaller acceleration.
Simplifying for a Solid Cylinder Yo-Yo
For a yo-yo modeled as a solid cylinder, the moment of inertia (I) is given by:
I = ½mr²
Substituting this into our acceleration equation, we get:
a = (2/3)g
This simplified equation shows that for a solid cylindrical yo-yo, the linear acceleration is (2/3) of the acceleration due to gravity.
Factors Affecting Yo-Yo Acceleration
Several factors influence a yo-yo's acceleration besides its mass and shape:
-
String Length: A longer string allows for a longer unwinding time and, consequently, a greater final velocity but doesn't directly impact the acceleration.
-
Friction: Air resistance and friction within the yo-yo's axle will slightly reduce the acceleration.
-
Yo-Yo Design: Different yo-yo designs (e.g., different mass distributions) have different moments of inertia and hence different accelerations.
Conclusion
Calculating the acceleration of a yo-yo involves understanding the interplay between gravitational force, tension, and rotational inertia. While the simplified model provides a good approximation, remember that real-world factors can slightly alter the calculated acceleration. This guide equips you with the fundamental knowledge and equations to analyze the physics of a yo-yo's motion. Experimenting with different yo-yos and measuring their acceleration can offer valuable insight into these principles.
Featured Posts
Also read the following articles
| Article Title | Date |
|---|---|
| How To Break Links In Excel And Keep Values Shortcut | Feb 24, 2025 |
| How To Change Name In Facebook Lite On Phone | Feb 24, 2025 |
| How To Negotiate Car Price When Financing | Feb 24, 2025 |
| How To Hold Red Wine Cup | Feb 24, 2025 |
| How To Find My Iphone Different Apple Id | Feb 24, 2025 |
Latest Posts
Thank you for visiting our website which covers about How To Find Acceleration Of Yoyo . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
