How To Find Area Of Triangle From Sides
Ronan Farrow
Feb 24, 2025 · 3 min read
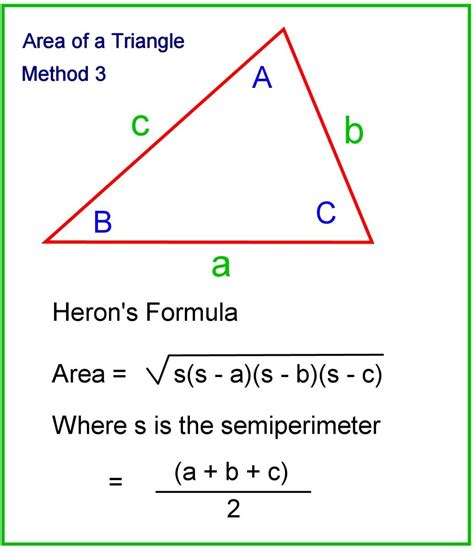
Table of Contents
How to Find the Area of a Triangle From Its Sides: A Complete Guide
Knowing how to calculate the area of a triangle is a fundamental concept in geometry with applications across various fields, from surveying to engineering. While the standard formula (½ * base * height) is straightforward when the height is known, it becomes trickier when you only have the lengths of the three sides. This is where Heron's formula comes into play. This comprehensive guide will walk you through understanding and applying Heron's formula to efficiently calculate the area of any triangle, regardless of its type (acute, obtuse, or right-angled).
Understanding Heron's Formula
Heron's formula provides a way to calculate the area of a triangle when you know the lengths of all three sides. It's named after Hero of Alexandria, a Greek engineer and mathematician. The formula is elegantly simple yet powerful:
Area = √[s(s-a)(s-b)(s-c)]
Where:
- a, b, c represent the lengths of the three sides of the triangle.
- s represents the semi-perimeter of the triangle, calculated as: s = (a + b + c) / 2
Step-by-Step Guide to Using Heron's Formula
Let's break down the process with a clear example. Let's say we have a triangle with sides:
- a = 5 units
- b = 6 units
- c = 7 units
Step 1: Calculate the semi-perimeter (s)
First, we find the semi-perimeter (s) by adding the lengths of all three sides and dividing the sum by 2:
s = (5 + 6 + 7) / 2 = 9 units
Step 2: Apply Heron's Formula
Now, plug the values of 's', 'a', 'b', and 'c' into Heron's formula:
Area = √[9(9-5)(9-6)(9-7)] = √[9 * 4 * 3 * 2] = √216 ≈ 14.7 square units
Therefore, the area of the triangle with sides 5, 6, and 7 units is approximately 14.7 square units.
Why Heron's Formula is Useful
Heron's formula offers a significant advantage: it bypasses the need to know the height of the triangle. This is especially useful in situations where:
- The height is difficult or impossible to measure directly. Imagine trying to find the area of a triangular plot of land; measuring its height might be impractical.
- You only have side lengths available. Many real-world applications provide side lengths as the primary available data.
Beyond the Basics: Applications and Further Exploration
Heron's formula is a cornerstone in various fields:
- Surveying: Calculating land areas.
- Engineering: Determining the area of triangular components in structures.
- Computer Graphics: Calculating areas of polygons for rendering and modeling.
Beyond its practical applications, exploring Heron's formula provides a deeper understanding of geometric relationships and mathematical problem-solving. It's a valuable tool for anyone looking to expand their mathematical knowledge and skills.
Conclusion
Heron's formula provides an efficient and versatile method for determining the area of a triangle using only its side lengths. This guide has provided a comprehensive step-by-step approach, making this powerful tool accessible to all. By understanding and applying Heron's formula, you'll be equipped to tackle a wide range of geometric problems and real-world applications. Remember to practice with different triangle dimensions to solidify your understanding and master this crucial geometric principle.
Featured Posts
Also read the following articles
| Article Title | Date |
|---|---|
| How To Increase Blood Pressure In Heart Failure | Feb 24, 2025 |
| How To Change Name In Facebook Desktop | Feb 24, 2025 |
| How To Block Tiktok Videos | Feb 24, 2025 |
| How To Lower Blood Pressure Holistically | Feb 24, 2025 |
| How To Evolve Riolu Heartgold | Feb 24, 2025 |
Latest Posts
Thank you for visiting our website which covers about How To Find Area Of Triangle From Sides . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
