How To Find Area Of Triangle With Just Side Lengths
Ronan Farrow
Feb 24, 2025 · 3 min read
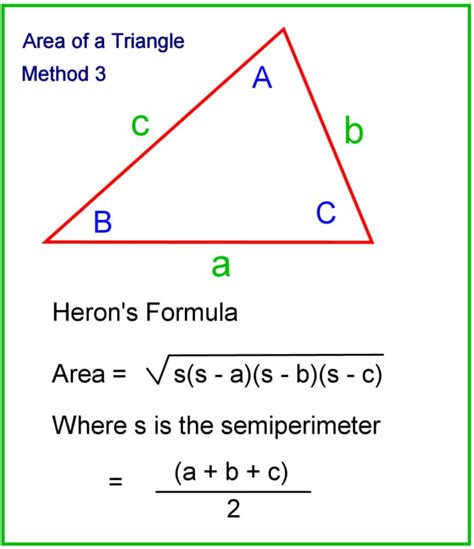
Table of Contents
How to Find the Area of a Triangle Knowing Only its Side Lengths: Heron's Formula Explained
Finding the area of a triangle is a fundamental concept in geometry, with applications ranging from basic surveying to advanced engineering. While the standard formula—base times height divided by two—is straightforward when the height is known, calculating the area when you only have the lengths of the three sides requires a different approach. This is where Heron's formula comes into play.
Understanding Heron's Formula
Heron's formula provides an elegant way to calculate the area of a triangle solely using the lengths of its three sides, often denoted as a, b, and c. It's particularly useful when the height of the triangle is not readily available or easily calculable. The formula is based on the concept of the semi-perimeter, denoted by 's'.
Calculating the Semi-perimeter (s)
The semi-perimeter is half the perimeter of the triangle. It's calculated as:
s = (a + b + c) / 2
Where:
- a, b, c represent the lengths of the three sides of the triangle.
Applying Heron's Formula
Once the semi-perimeter is determined, Heron's formula can be used to calculate the area (A) of the triangle:
A = √[s(s - a)(s - b)(s - c)]
This formula provides a direct calculation of the area using only the side lengths and the semi-perimeter. Let's break down the steps with an example.
Step-by-Step Example: Finding the Area of a Triangle
Let's say we have a triangle with sides of length:
- a = 5 units
- b = 6 units
- c = 7 units
Step 1: Calculate the semi-perimeter (s)
s = (5 + 6 + 7) / 2 = 9 units
Step 2: Apply Heron's Formula
A = √[9(9 - 5)(9 - 6)(9 - 7)] = √[9 * 4 * 3 * 2] = √216 ≈ 14.7 square units
Therefore, the area of the triangle with sides 5, 6, and 7 units is approximately 14.7 square units.
Why Heron's Formula is Important
Heron's formula provides a powerful tool for solving various geometric problems. Its ability to calculate the area using only side lengths makes it indispensable in situations where the height of the triangle is difficult or impossible to determine directly. This makes it invaluable in fields like:
- Surveying: Calculating land areas based on measured side lengths.
- Engineering: Determining the area of triangular structures or components.
- Computer graphics: Calculating areas within polygonal models.
Beyond the Basics: Expanding your Knowledge
While Heron's formula provides a direct method for calculating the area, understanding the underlying geometric principles is crucial. Exploring related concepts such as the trigonometric approach to area calculation and understanding the limitations of Heron's formula (for degenerate triangles with collinear vertices) can further enhance your geometrical understanding.
By mastering Heron's formula, you unlock a powerful tool for solving a wide range of geometric problems efficiently and accurately. Remember to practice with various examples to solidify your understanding and gain confidence in applying this valuable method.
Featured Posts
Also read the following articles
| Article Title | Date |
|---|---|
| How To Lower Cholesterol Johns Hopkins | Feb 24, 2025 |
| How To Make Whatsapp Sticker Using Video | Feb 24, 2025 |
| How To Increase Battery Health Iphone 11 Pro Max | Feb 24, 2025 |
| How To Make Google Form Single Choice | Feb 24, 2025 |
| How To Block Tiktok Videos | Feb 24, 2025 |
Latest Posts
Thank you for visiting our website which covers about How To Find Area Of Triangle With Just Side Lengths . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
