How To Find Lcm Of Decimal Numbers
Ronan Farrow
Feb 24, 2025 · 3 min read
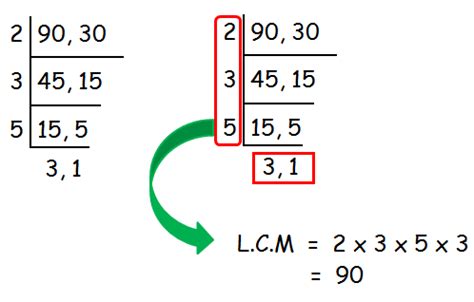
Table of Contents
How to Find the LCM of Decimal Numbers: A Comprehensive Guide
Finding the least common multiple (LCM) of decimal numbers might seem daunting at first, but it's a manageable process once you understand the underlying principles. This guide will break down the steps, offering a comprehensive approach to calculating the LCM of decimals.
Understanding the Fundamentals
Before diving into the calculations, let's refresh our understanding of key concepts:
-
Least Common Multiple (LCM): The smallest positive number that is a multiple of two or more numbers. For example, the LCM of 2 and 3 is 6.
-
Decimal Numbers: Numbers containing a decimal point, representing a fraction. For example, 2.5 is a decimal number.
Converting Decimals to Fractions: The Crucial First Step
The key to finding the LCM of decimal numbers lies in converting them into fractions. This allows us to leverage established methods for finding the LCM of fractions.
Step-by-Step Conversion
-
Identify the decimal number: Let's say we have the decimal number 2.5.
-
Express as a fraction: 2.5 can be written as 25/10 (twenty-five tenths).
-
Simplify the fraction (if possible): 25/10 simplifies to 5/2.
Repeat this process for all decimal numbers involved in your LCM calculation.
Calculating the LCM of Fractions
Once you've converted your decimal numbers to fractions, you can use the following method to find their LCM:
-
Find the prime factorization of each numerator and denominator: This means expressing each number as a product of its prime factors. For example, the prime factorization of 12 is 2 x 2 x 3 (or 2² x 3).
-
Identify the highest power of each prime factor: Look at all the prime factors present in all the numerators and denominators. Select the highest power of each.
-
Multiply the highest powers together: The product of these highest powers is the LCM of the denominators.
-
Find the LCM of the numerators: Use the same prime factorization method as described above to find the LCM of the numerators.
-
Combine the results: The LCM of the fractions is the LCM of the numerators divided by the LCM of the denominators.
Example Calculation
Let's find the LCM of 2.5 and 1.25.
-
Convert to fractions: 2.5 = 5/2 and 1.25 = 5/4
-
Prime factorization of numerators: Both numerators are 5, which is a prime number.
-
Prime factorization of denominators: 2 = 2 and 4 = 2 x 2 = 2²
-
Highest power of prime factors: The highest power of 2 is 2², and the highest power of 5 is 5.
-
LCM of denominators: 2² = 4
-
LCM of numerators: 5 (since both numerators are 5)
-
LCM of fractions (and therefore decimals): LCM of numerators / LCM of denominators = 5 / 4 = 1.25
Therefore, the LCM of 2.5 and 1.25 is 2.5.
Handling More Complex Scenarios
The method outlined above can be applied to any number of decimal numbers. For more complex scenarios with many decimals, a systematic approach using prime factorization will ensure accurate results.
Conclusion
Finding the LCM of decimal numbers is a straightforward process once you understand the steps involved. By converting decimals to fractions and applying the prime factorization method, you can efficiently calculate the LCM of any set of decimal numbers. Remember to take your time, be methodical, and break the problem down into manageable steps. This will help build your understanding and confidence in tackling these types of mathematical problems.
Featured Posts
Also read the following articles
| Article Title | Date |
|---|---|
| How To Introduce Yourself In Reporting In Class | Feb 24, 2025 |
| How To Get Taller For Kids | Feb 24, 2025 |
| How To Lower Cortisol When Stressed | Feb 24, 2025 |
| How To Delete Google Business Account From Mobile | Feb 24, 2025 |
| How To Egg Boil | Feb 24, 2025 |
Latest Posts
Thank you for visiting our website which covers about How To Find Lcm Of Decimal Numbers . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
