How To Factorize Quadratic Equations
Ronan Farrow
Feb 24, 2025 · 3 min read
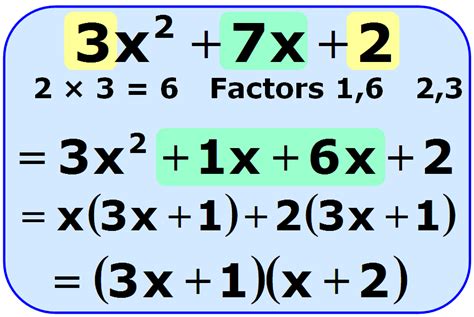
Table of Contents
How to Factorize Quadratic Equations: A Complete Guide
Quadratic equations are a fundamental concept in algebra, and knowing how to factorize them is a crucial skill for solving them and tackling more advanced mathematical problems. This comprehensive guide will walk you through the process, providing clear explanations and practical examples.
Understanding Quadratic Equations
A quadratic equation is an equation of the form ax² + bx + c = 0, where 'a', 'b', and 'c' are constants, and 'a' is not equal to zero. The highest power of the variable 'x' is 2, hence the term "quadratic." Solving these equations means finding the values of 'x' that make the equation true. Factoring is one common method for achieving this.
Methods for Factorizing Quadratic Equations
There are several techniques for factorizing quadratic equations. Let's explore the most common ones:
1. Finding Common Factors
This is the simplest method. If all three terms (ax², bx, and c) share a common factor, you can factor it out.
Example: 2x² + 4x + 6 = 0
Here, 2 is a common factor: 2(x² + 2x + 3) = 0
While this doesn't fully solve the equation, it simplifies it. Further factoring may or may not be possible depending on the expression inside the parentheses.
2. The AC Method (for equations where a ≠ 1)
This is a powerful method for factorizing quadratic equations where the coefficient of x² (a) is not 1.
Steps:
- Multiply 'a' and 'c': Find the product of the coefficient of x² and the constant term.
- Find two numbers: Find two numbers that add up to 'b' (the coefficient of x) and multiply to the product you calculated in step 1.
- Rewrite the equation: Rewrite the middle term (bx) as the sum of the two numbers you found.
- Factor by grouping: Group the terms in pairs and factor out common factors from each pair.
- Factor out the common binomial: You should now have a common binomial factor that you can factor out.
Example: 3x² + 7x + 2 = 0
- ac = 3 * 2 = 6
- Two numbers: The numbers 6 and 1 add up to 7 and multiply to 6.
- Rewrite: 3x² + 6x + 1x + 2 = 0
- Factor by grouping: 3x(x + 2) + 1(x + 2) = 0
- Common binomial: (3x + 1)(x + 2) = 0
3. The Difference of Squares
This method applies specifically to quadratic equations of the form a² - b² = (a + b)(a - b).
Example: x² - 9 = 0
This can be rewritten as x² - 3² = 0, which factors to (x + 3)(x - 3) = 0
4. Perfect Square Trinomials
A perfect square trinomial is a quadratic equation that can be factored into the form (a + b)² or (a - b)². Recognizing this pattern simplifies the factorization process.
Example: x² + 6x + 9 = 0
This is a perfect square trinomial and factors to (x + 3)² = 0
Solving the Equation After Factorization
Once you've successfully factorized the quadratic equation, you can solve for 'x' by setting each factor equal to zero and solving the resulting linear equations.
Example: (x + 3)(x - 2) = 0
This gives you two solutions: x + 3 = 0 => x = -3 and x - 2 = 0 => x = 2
Practice Makes Perfect
Mastering factorization takes practice. Work through numerous examples, gradually increasing the complexity of the quadratic equations. Start with simpler equations and progressively tackle more challenging ones. The more you practice, the quicker and more accurate you'll become at identifying the best method for each equation.
This complete guide provides a solid foundation for factorizing quadratic equations. Remember to practice consistently to improve your skills and confidence in solving these crucial algebraic expressions.
Featured Posts
Also read the following articles
| Article Title | Date |
|---|---|
| How To Connect Airpods To Windows Laptop Youtube | Feb 24, 2025 |
| How To Negotiate Buying A New Car | Feb 24, 2025 |
| How To Know Your Face Shape Male App | Feb 24, 2025 |
| How To Get Rid Of Dark Eye Circles At Home | Feb 24, 2025 |
| How To Delete Airdrop History | Feb 24, 2025 |
Latest Posts
Thank you for visiting our website which covers about How To Factorize Quadratic Equations . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
